今日内训主要介绍两篇一脉相承的文章:
- Deep-Learning Inversion of Seismic Data:地震数据在输入到网络之前会经过了一系列嵌入手段来对数据的空间进行了重构 (编码),并通过DNN来进行空间对齐,最后用CNN对对齐数据进行训练 (解码)。
- Deep-learning seismic full-waveform inversion for realistic structural models:
- 在原SeisInvNet网络基础上,扩宽了嵌入操作维度范围,在一定程度上提升了SeisInvNet的效果,同时,提出了更多的模拟地层结构的仿真手段来弥补原SeisInvNet的泛化性不足的问题。
符号定义
首先对一些反演过程中所引入的符号进行定义:
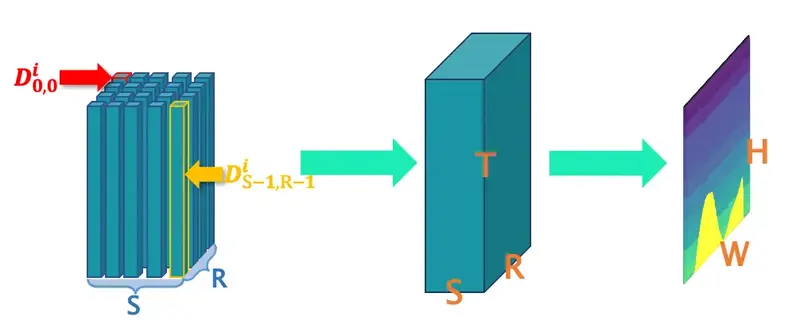 反演过程
反演过程
- 地震数据的大小为,其中、和分别表示震源个数、接收器个数和时间步长的数量。
- 速度模型的大小为,分别表示速度模型的高度和宽度。
网络分析
现存问题
对于深度学习主导的FWI任务,可以简化为下述映射:
主流模型大多采用基于CNN的一些网络结构来构造这种映射。但在这两篇文章中,作者认为直接采用CNN并不是最佳的选择,理由如下:
- 空间对应性弱,速度模型中的界面与地震数据中的对应模式具有较弱的空间对应关系。
- 地震数据与速度模型的不确定反射-接收关系。
因此,作者希望通过嵌入和DNN特征提取等一些手段替代CNN对于地震图像的前期编码的处理,缓解了CNN对于反射-接收关系的不确定性。
解决方案
作者通过引入嵌入操作和对齐特征图两个中间状态,来替代地震图像的前期编码。
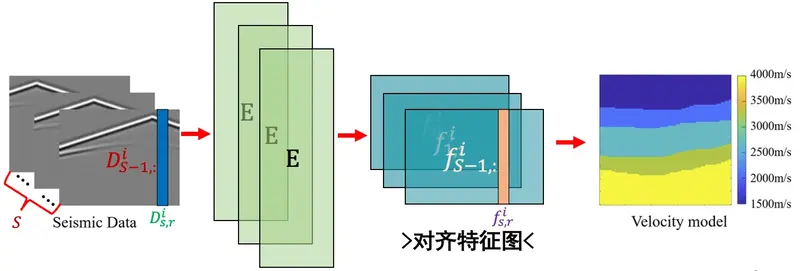 嵌入手段的DL-FWI
嵌入手段的DL-FWI
映射表示如下:
嵌入过程
对于嵌入向量,计算方式如下:
每个分量包含了不同的信息。
邻域信息
邻域信息分别提取同炮面的地震道(s相等)和同接收器的地震道(r相等)的信息,分别进行CNN后获得邻域信息、,最后提取所在接收器/炮面的一道数据、。
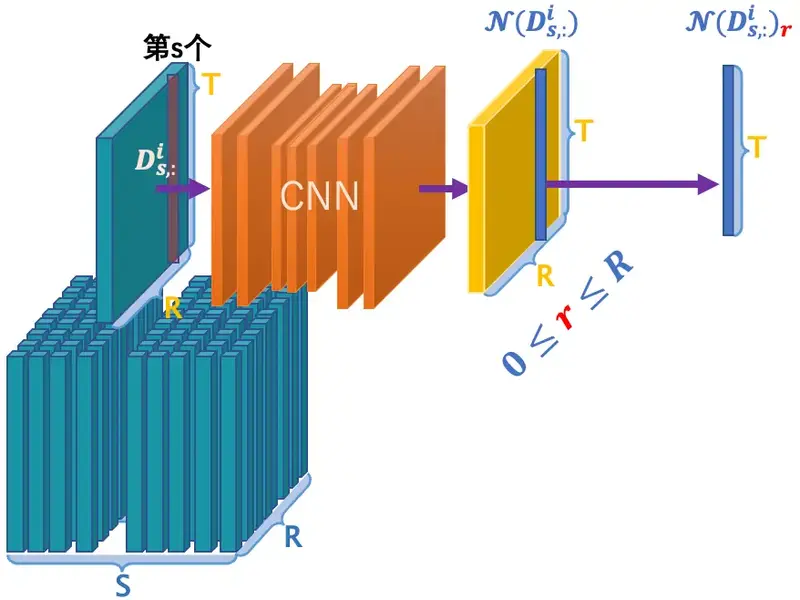 邻域信息计算-同炮面提取
邻域信息计算-同炮面提取
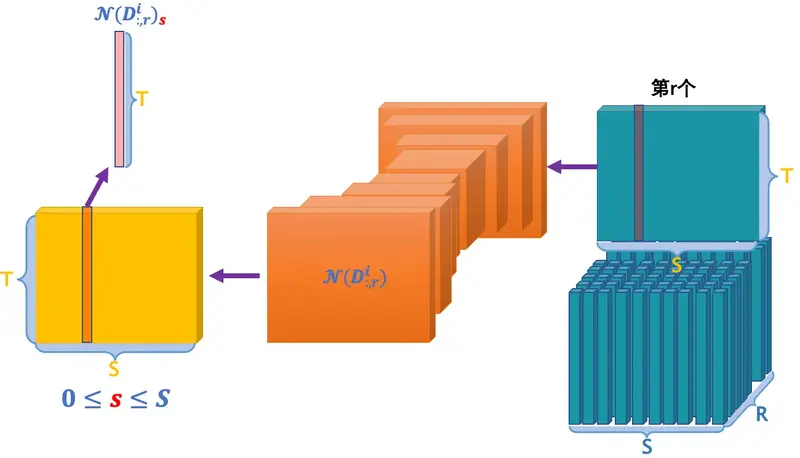 邻域信息计算-同接收器提取
邻域信息计算-同接收器提取
最后,将两者进行矩阵加操作,得到最终的邻域信息。
全局上下文
全局上下文所提取的地震道与上述一致,不同的是提取地震道并进行CNN计算后获取的向量尺寸为,表示了所在炮面/接收器的全局信息。
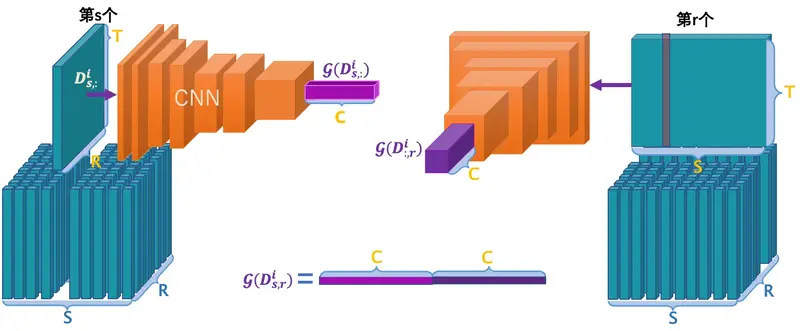 全局上下文
全局上下文
观测设置
观测设置由两个one-hot编码组成,分别表示地震道所在炮面/接收器的编号。最后将两者concatenate为的向量。
空间对齐
空间对齐过程是全连接神经网络,对每一道地震数据进行计算,过程如下图所示:
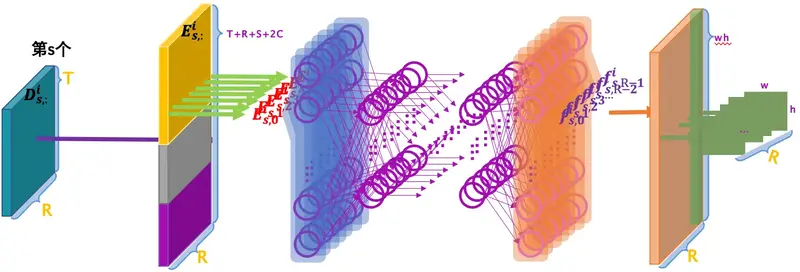 空间对齐
空间对齐
卷积映射
卷积映射的网络结构与先前介绍的InversionNet类似,通过最后的端到端的CNN后,我们就能获得一个的速度模型。
这样,全过程示意如下:
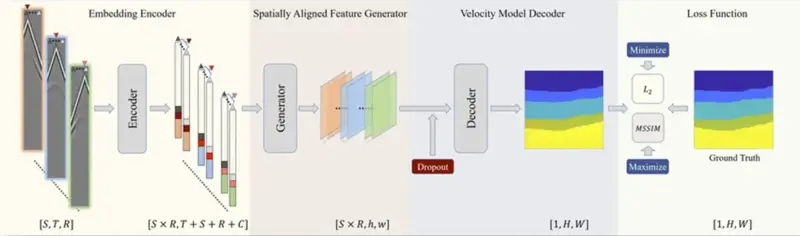 网络概览
网络概览
Comments